Предельная теорема и предельная ошибка

Сущность предельных теорем состоит в том, что в массовых явлениях совокупное влияние различных случайных причин на формирование закономерностей будет малой величиной или практически не зависит от случая.

Поскольку случайная ошибка выборки возникает в результате случайных различий между единицами выборочной и генеральной совокупностей, то при достаточно большом объеме выборки она будет сколь угодно мала.

Под средней (стандартной) ошибкой выборки понимают такое расхождение между средней выборочной и генеральной совокупностью:

которое не превышает ±Δ.

Обозначения основных характеристик параметров генеральной и выборочной совокупности приведены в табл. 7.3.

Предельной ошибкой выборочного наблюдения называется разность между величиной средней в генеральной совокупности и ее величиной, вычисленной по результатам выборочного наблюдения:

Доказано, что величина предельной ошибки выборки не должна превышать соотношения

где величина μ называется средним квадратическим отклонением выборочной средней от генеральной средней и (средняя ошибка выборки) определяется по зависимости

где

— среднее квадратическое отклонение в генеральной совокупности;

n — число наблюдений;

t — коэффициент доверия, параметр, указывающий на конкретное значение вероятности того, на какую величину генеральная средняя будет отличаться от выборочной средней.

Как правило, именно произведение коэффициента доверия на среднюю ошибку выборки и рассматривают в качестве предельной ошибки, что является более строгим и правильным, а разность генерального и выборочного среднего рассматривают просто как ошибку выборки, являющуюся случайной величиной.

В некоторых случаях величину

называют также средней ошибкой выборки и также обозначают μ.

Соотношение между дисперсиями генеральной и выборочной совокупности выражается формулой

Поскольку величина (n / n – 1) при достаточно больших n близка к 1, то можно приближенно считать, что выборочная и генеральные дисперсии равны.

Составлены специальные таблицы, связывающие коэффициент доверия t с вероятностью того, что разность между выборочной и генеральной средними не превысит значения средней ошибки выборки μ:

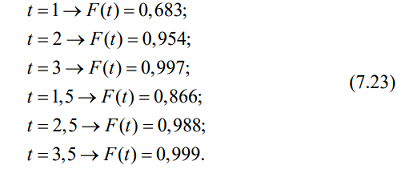
Из первой строки видно, что с вероятностью 0,683 можно утверждать, что разность между выборочной и генеральной средними не превысит одной величины средней ошибки выборки.

Далее видно, что чем больше пределы, в которых допускается возможная ошибка, тем с большей достоверностью судят о ее величине.